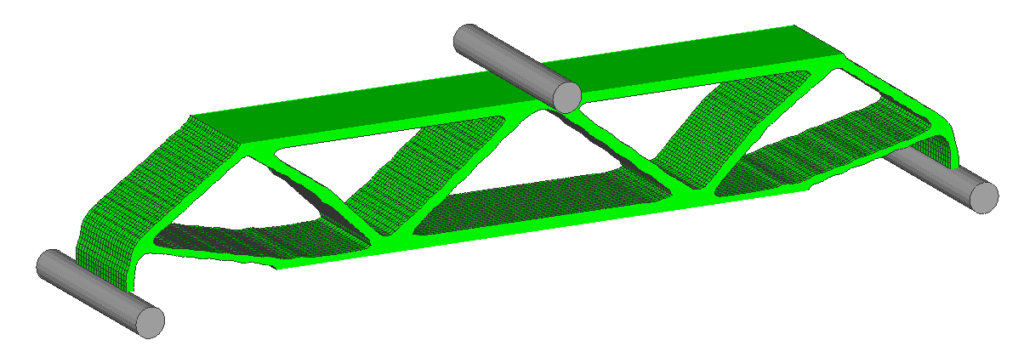
本事例のトピック
- 構造解析最適化において省略されがちな「接触境界条件」の重要性を検証するため、単純な3点曲げ梁モデルを用いて「非線形接触(接触・乖離あり)」と「接着(線形結合)」によるトポロジー最適化結果の違いを比較
- 一般的な線形トポロジー最適化では考慮できない接触状態の変化(Gap/Slide)を計算ループ内に組み込むことで、治具との接触部における回転や浮き上がりを正確に再現し、現実に即した最適なトラス形状を導出
- 境界条件を簡易化(接着)した場合、現実とは異なるロードパス(軸と治具が一直線に繋がる等)が形成され、「計算上は強いが実際には役に立たない形状」が生成されるリスクを定量的に提示
今回のトポロジー最適化受託設計事例では、非線形接触を使用したトポロジー最適化の事例を紹介します。
技術解説:「線形結合」と「非線形接触」は何が違うのか?
CAE解析において、部品と部品のつなぎ目をどう定義するかは、計算コストと精度のトレードオフとなります。
× 線形結合 (Linear Glue/Tie)
節点共有やMPC(多点拘束)により、接合面を完全に固着させる手法。
【物理的意味】 溶接や接着。
【最適化のリスク】 引張・圧縮・せん断のあらゆる力を伝達できるため、ソルバーが「実際には離れてしまう場所」にも強引にロードパスを通してしまい、現実には成立しない形状が生成される。
◎ 非線形接触 (Non-linear Contact)
部品間の「乖離(Gap)」や「滑り(Slide)」を許容する手法。
【物理的意味】 接触・摩擦。
【最適化のメリット】 「押す力(圧縮)」は伝わるが「引く力(引張)」では離れるという現実の物理現象(Status Change)を計算ループ内で更新し続けるため、真に必要なリブ配置のみが導出される。
一般的なトポロジー最適化ソフトの多くは、計算安定性の観点から「線形結合」を前提としていますが、本事例で用いるGENESIS等は、この接触状態の変化を考慮しながら形状を探索できる数少ないソルバーの一つです。
単純な3点曲げ梁計算のモデルをまずは用意しました。条件は以下のようになっています。
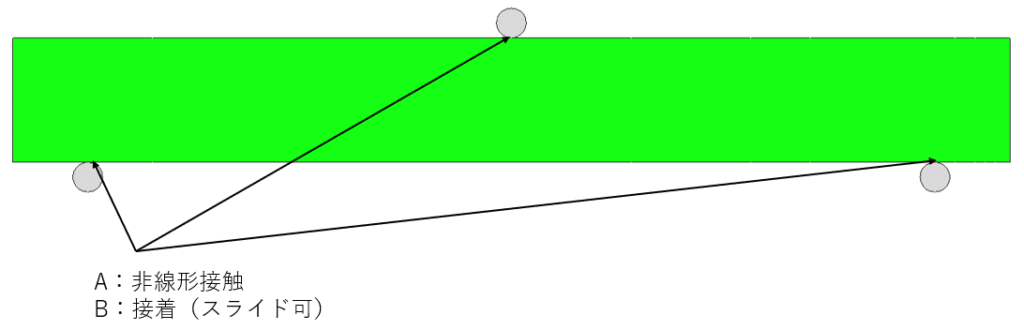
一つは接着とし、もう一つは非線形接触として計算する。
上記のように、違いを確認するために梁と治具の間は、
A.非線形接触
B.接着(スライド可)
上記の2パターンの境界条件を用意しました。もちろん、実現象に近いのはAの非線形接触となります。最適化前の計算結果を確認してみましょう。

接着モデルは明らかに現実世界ではあり得ない変形モードになっており、非線形接触モデルは正しい変形モードになっている。
この非線形接触を考慮した解析はほとんどのCAEソルバーで計算が可能。(最適化で使用できるソルバーはほとんど存在しない)
変形スケール、コンタースケールはどちらも同じです。境界条件違いによる計算結果を確認すると、Bの接着(スライド可)は明らかに実現象とは違った挙動を示しており、変形モードも応力分布も適切とは言えない結果となりました。
それぞれの境界条件を使用して、トポロジー最適化を実行してみましょう。単純比較しやすいように、押出し形状の制約条件を使用しています。
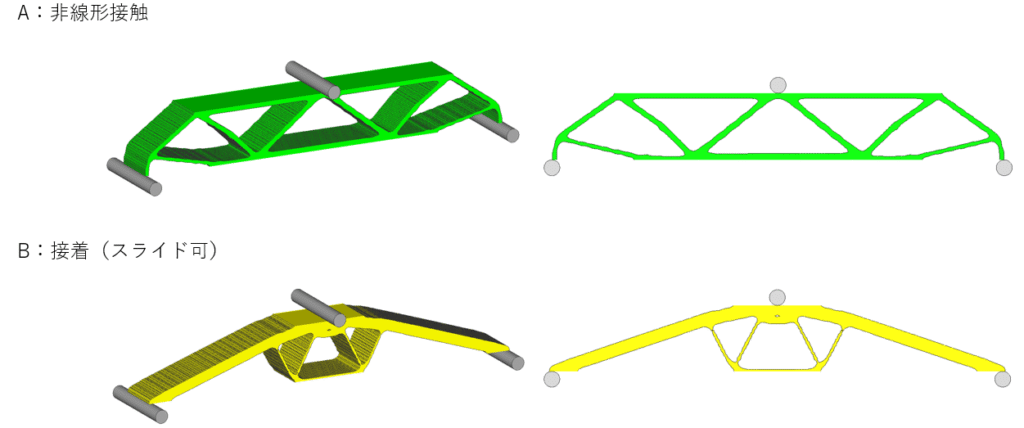
接着モデルは治具と梁の滑りや回転を考慮しないため、固定部と入力部を直線で接続してしまう。
一方の非線形接触モデルは現実的な形状となり、実在する橋のような形状となる。
境界条件の違いにより、全く異なる形状に収束しました。Aの非線形接触を境界条件として使用したトポロジー最適化結果では、荷重を受ける部分をトラス構造として強く意識していることがわかります。一方、Bの接着(スライド可)の方は、固定治具(丸棒)部分の接触が回転しないため、軸と圧子を一直線に繋ぐ結果となっています。
Tips:
非線形接触モデルの治具接触面が小さくなってしまう現象は、Frozenという設定で接地範囲を削除しないように拘束することが可能です。
このように、境界条件の違いにより大きく最適化形状が変化してしまうことがわかる結果となりました。CAEによる最適化を実行する際は、荷重条件を抜け漏れなくすることだけでなく、境界条件も適切な条件にすることが大切であることがわかります。
残念ながら、構造解析単独では非線形接触が使用できても、最適化解析では非線形接触が考慮できない最適化ソルバーがあり、正しい最適化結果を導出できないことがあります。最適化結果が間違えているのでは?感じたら、条件設定をよく確認してみるといいかもしれませんね。
その解析課題、GRMが解決します。
本記事でご紹介した「非線形接触を考慮した最適化解析」や「正しい境界条件での最適化解析」を、御社の製品開発に適用しませんか?
「現状のモデルを見てほしい」「テスト解析を依頼したい」など、技術的なご相談からでも大歓迎です。
※「記事を見た」と書いていただけるとスムーズです。
※技術のご相談は各事例モデルの解析担当者に対応させます。
この記事の監修・執筆チーム
GRM Consulting株式会社 解析エンジニアリング部
モータースポーツ最高峰のF1から量産車開発まで、20年以上にわたり構造設計・衝突・振動・流体解析に携わるスペシャリスト集団。 単なるシミュレーション結果の提示に留まらず、本記事のような高度な最適化設計を得意とし、製造要件(鋳造・鍛造・押出成形・板金・CFRP)を考慮した「造れる設計」を提案しています。
- 主要ツール:LS-DYNA, Abaqus, Genesis, Nastran, OptiAssist, Simcenter 3D
- 専門領域:構造最適化、衝撃エネルギー吸収体最適化、CFRP複合材解析、衝突解析、CFD解析
