本事例のトピック
- ロケットのフェアリングや圧力容器など、薄肉構造において致命的な破壊モードとなる「円錐殻の座屈(Shell Buckling)」に対し、GENESISソルバーを用いた最適化で対策案を導出
- 多くの最適化ツールで制御が難しい「座屈固有値係数(Buckling Load Factor)」を設計応答(制約条件)として直接定義し、トポメトリー最適化により目標値(係数1.2以上)を満足する板厚分布を決定
- 製造要件を考慮し、円周方向には板厚を一定に保ちつつ、軸方向に対して最適な板厚勾配を持たせることで、旋盤加工等で製作可能な現実的な補強形状を実現
今回の事例では、柱の座屈問題を最適化した事例でも少し触れた、円錐殻の座屈について紹介します。
使用するモデルは以下のようなモデルです。
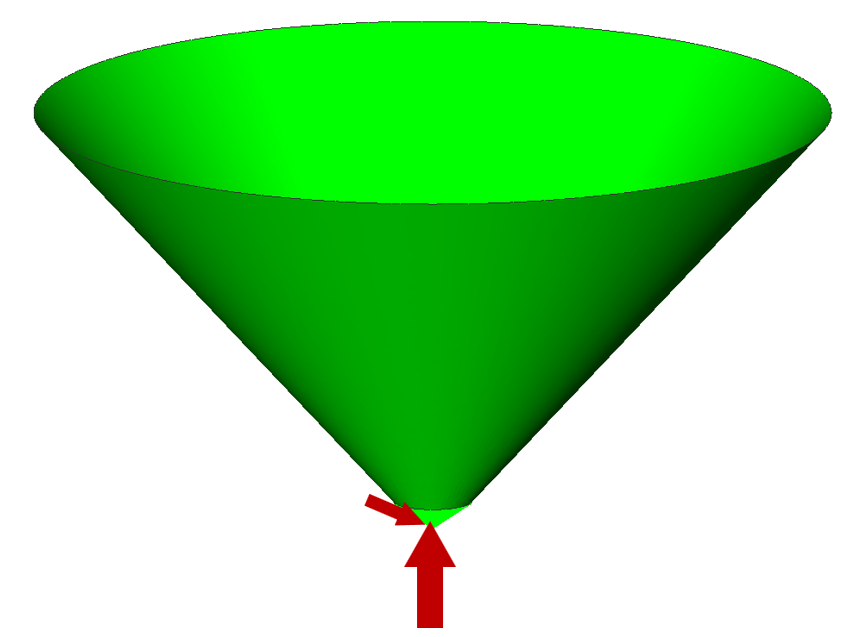
設計が非常に難しい円錐殻の座屈をCAE最適化設計でコントロールするためのモデル。
軸方向荷重と、軸直交方向荷重を与えます。軸直交方向荷重は、軸方向荷重の1/10の大きさです。コーン(円錐殻)の上辺をSPCで拘束しています。
技術解説:なぜ「円錐殻の座屈」は設計者を悩ませるのか?
円筒や円錐といった「シェル構造」の座屈設計は、梁(ビーム)の座屈とは比較にならないほどの難易度を伴います。その主な理由は以下の2点です。
1. 初期不整感度 (Imperfection Sensitivity)
シェル構造は、製造時に生じるごくわずかな形状誤差(初期不整)によって、座屈荷重が理論値(線形座屈解)から激減する特性があります。 そのため、実際の設計では「ノックダウン係数 (Knockdown Factor)」と呼ばれる安全率(NASA SP-8007等では係数0.1~0.6程度)を見込む必要があり、これが過剰設計(重量増)の温床となります。
2. モードの密集と入れ替わり (Mode Crossing)
薄肉シェルは類似した座屈固有値を持つモードが多数存在(密集)します。 特定のモードだけを対策しても、最適化の過程で「別のモードが主役に躍り出る(モードスイッチング)」現象が頻発し、いたちごっこになりがちです。
本事例で用いるGENESISのトポメトリー最適化は、数千~数万の設計変数を同時に制御することで、この「モードの入れ替わり」を数学的に封じ込め、初期不整の影響を受けにくい堅牢なリブ配置や板厚分布を導き出します。
早速、座屈固有値を確認してみましょう。
使用するソルバーはGenesis2024.1を使用し、線形解析で座屈固有値係数を求めます。

初期設計の座屈固有値係数は0.6であり、強度/剛性が一見満足しているようでも実際には座屈してしまう。
座屈固有値係数は0.6でした。入力荷重の60%程度で座屈してしまうことがわかります。
ここから、座屈固有値係数を1.2になるように最適化していきます。今回の最適化では、コーン(円錐殻)の板厚をトポメトリー(Topometry)最適化で変更します。トポメトリー最適化では、任意の分割指定に合わせて、部分部分で板厚を変更する最適化です。CFRPなどの板厚可変が容易な製品では一般的な最適化手法です。トポロジー最適化も組み合わせて、Solid形状による補強や穴あけも同時に検討できますが、今回は割愛します。
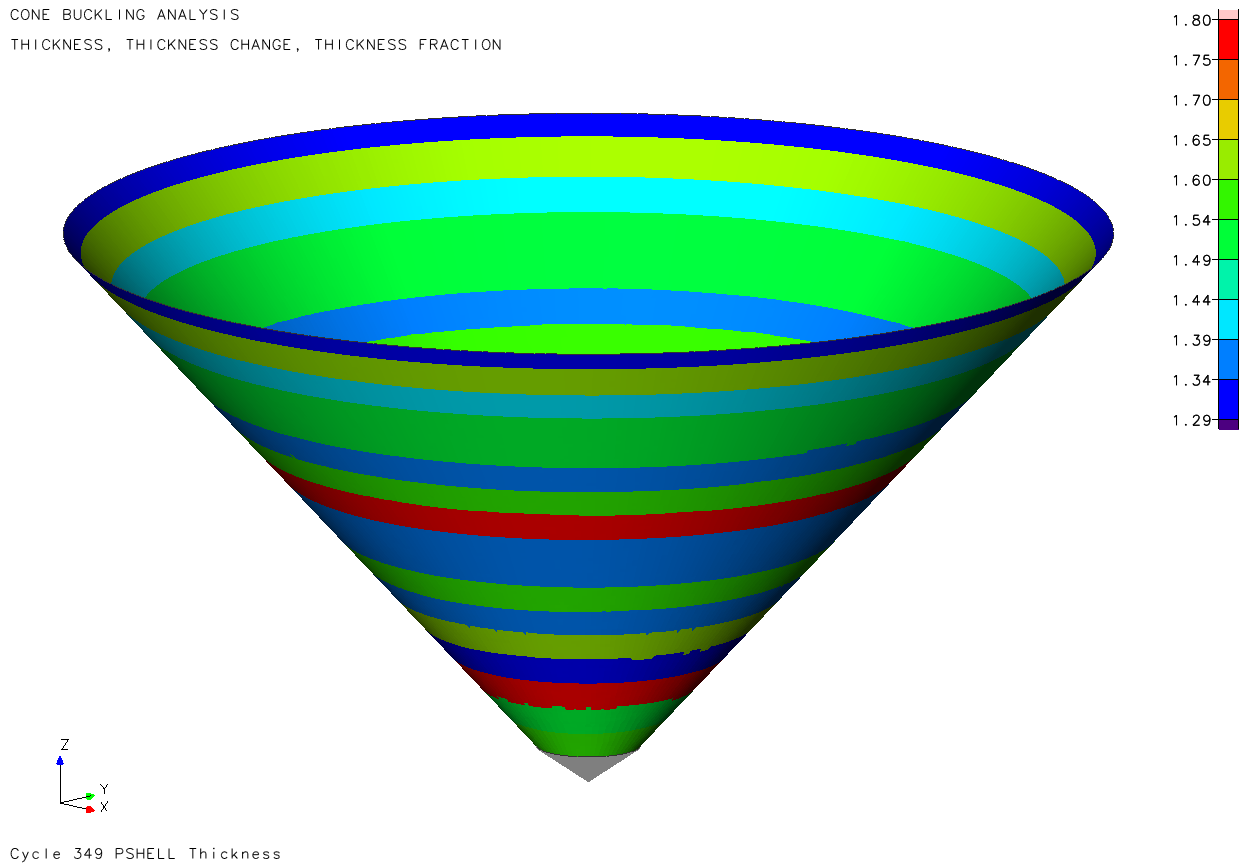
円錐殻の座屈固有値係数を1.2となるように設計した円錐殻(コーン)の板厚分布。
最適化後の板厚分布マップが上図となります。最大板厚は1.8mm、最小板厚は1.3mmです。トポメトリー最適化の設定で、円周方向に板厚一定になるように指定したため、旋盤加工で製作できる板厚分布になっています。デモ用モデルのためメッシュが粗く、板厚分布がスムーズではありませんがデモモデルのためご容赦ください。円柱や円錐形状では、メッシュサイズやメッシュ分布が座屈に対して敏感なため、実際の製品設計では気を遣う部分になります。
トポメトリー最適化による板厚変化は、今回の円周方向に一定以外にも、放射状の板厚分布にしたりランダムな板厚分布にしたりユーザーが自由に指定することが可能です。
また、この板厚はコーンの最外形をキープしたまま、コーンの内側に向かって板厚が増えるように設定されています。そのため、板厚を付与した3Dデータを作成すると、コーンの外側は一定面となり、内側は凹凸のある形状になります。
最適化後モデルのコーンの座屈固有値係数は制約条件どおり、1.2となりました。以下が最適化後の座屈CAE解析結果です。(あまり変わり映えしませんね)

円錐殻の座屈固有値係数は1.2となっており、制約条件を満たしていることが確認できた。
せっかくなので、こちらのモデルを使用して、LS-Dynaで座屈の様子を確認してみましょう。入力条件としてはImplicitソルバーを使用した方がいいのですが、今回はあくまで座屈の様子が見たいためExplicitを使用しています。
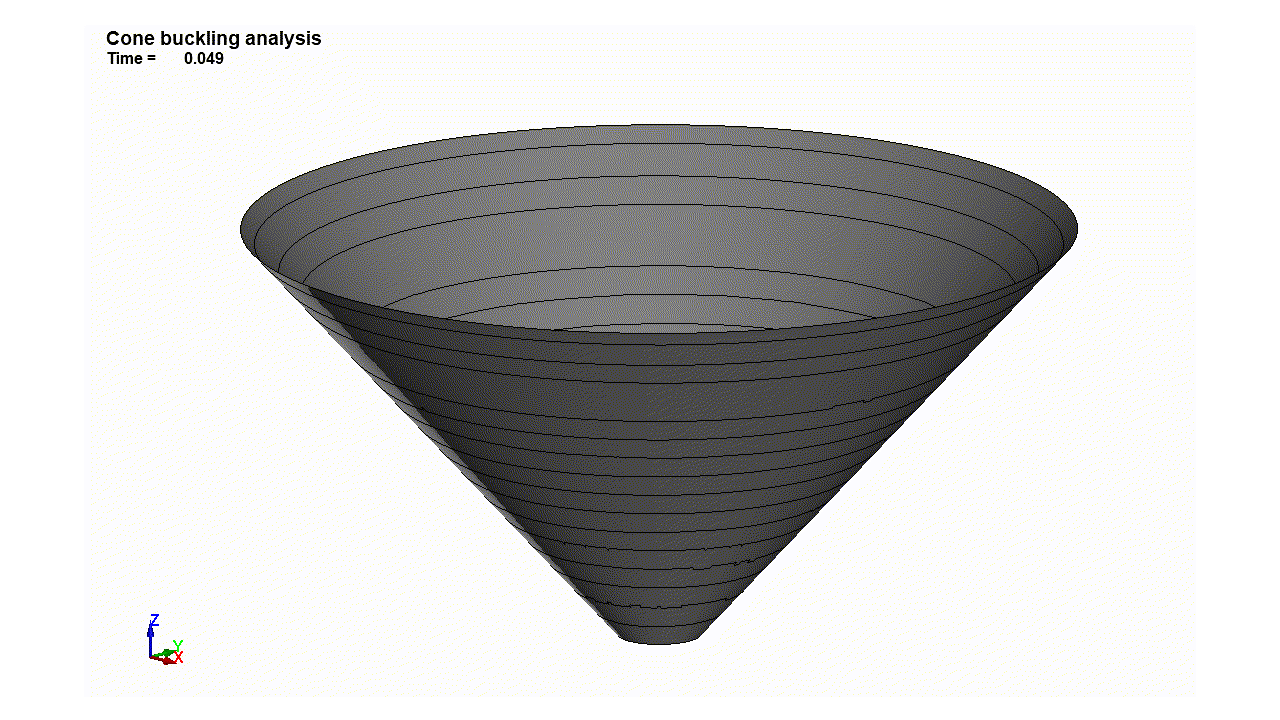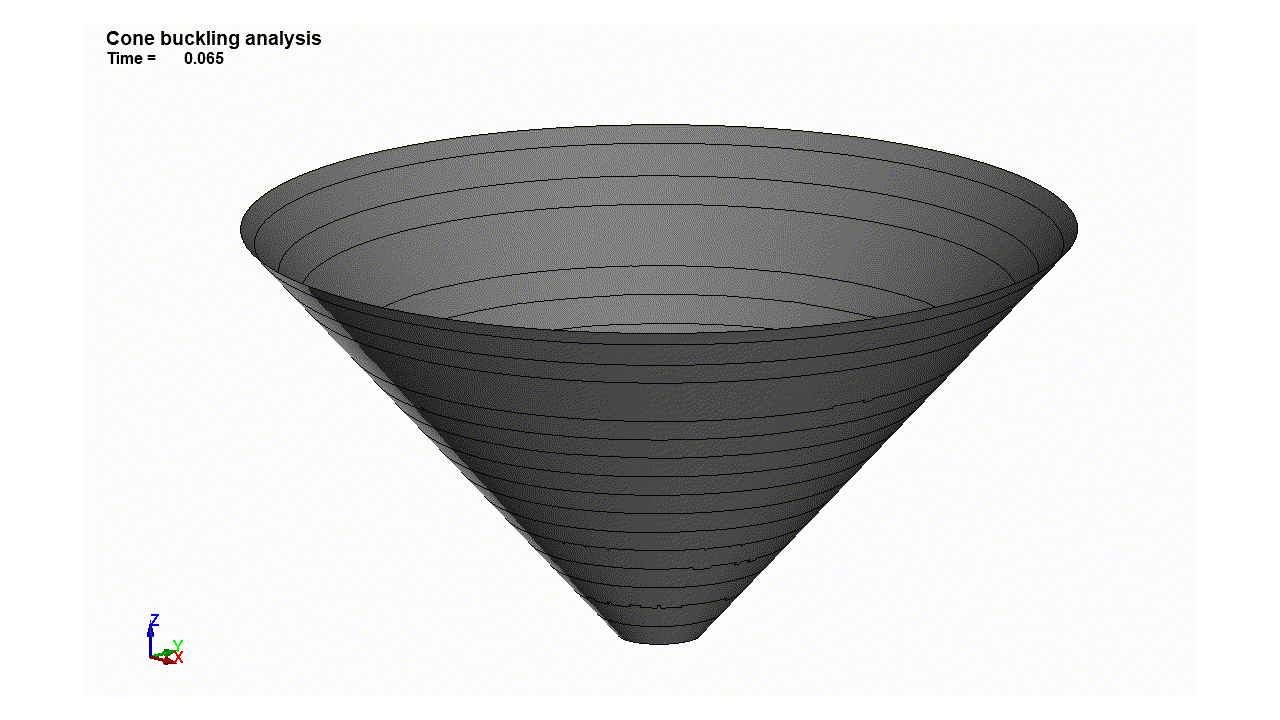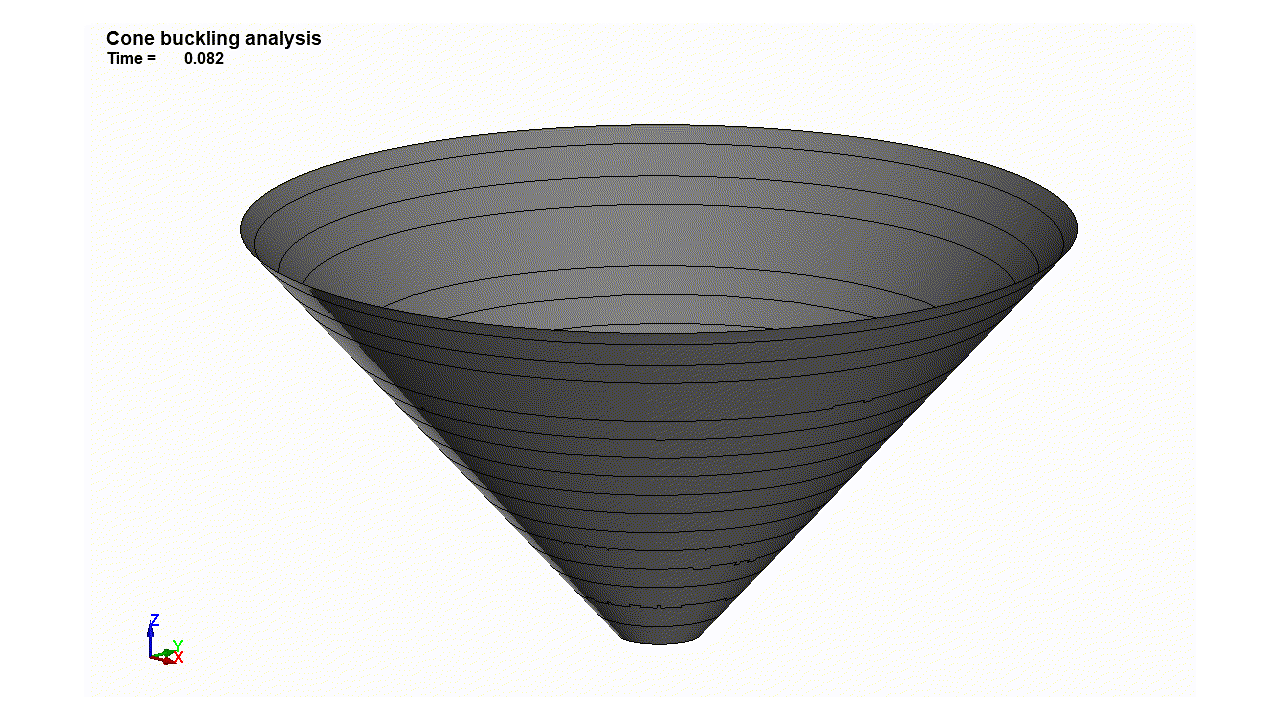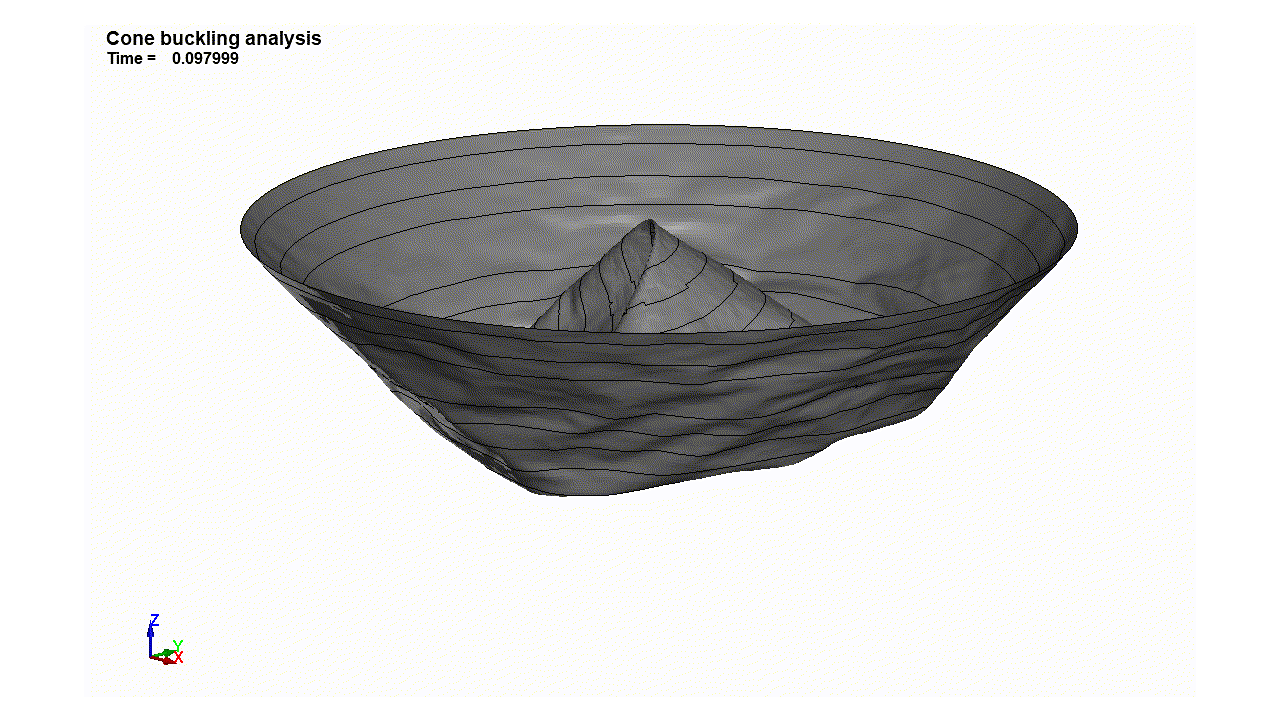
Genesisによる解析結果どおり1.2倍荷重に至った瞬間に円錐殻表面に凹凸が現れる。その後は一気に崩壊してしまう。
最大荷重に至った瞬間、コーン表面に凹凸が現れ、大きな変形をします。線形解析ではよくわからない座屈モードの様子が確認できました。
今回は取り扱いませんが、殻の座屈問題は形状初期不整などの所謂バラツキに敏感であり、大きく座屈荷重が変化してしまうため、実務では注意が必要です。
また、最適化初期状態(Cycle0)の状態によっても最適化結果が大きく変化するためこちらも注意が必要です。今回はMultiRunという機能を使用しているため、詳しくはMultiRunの事例をご覧ください。
技術Tips:初期値依存性を打破する「MultiRun」機能
本事例のような「座屈固有値」や「CFRPの積層順序」を扱う最適化問題は、設計変数のわずかな違いで結果が大きく変わる「初期値敏感性」が高い課題として知られています。
局所解(Local Minima)の罠:
一般的な最適化アルゴリズムは、計算開始地点(初期値)から「登りやすい山」を登ってしまうため、近くにある低い山頂(局所解)で計算を終了してしまうリスクがあります。特に座屈モードが複雑に入れ替わる問題では、この傾向が顕著です。
GENESISの解決策「MultiRun」:
そこで今回は、GENESIS独自の「MultiRun」機能を使用しました。
これは、乱数を用いて異なる初期値を持つ複数の最適化計算を自動で並列実行し、それらの中からベストな解(大域解の候補)を抽出する機能です。
これにより、設計者の勘に頼ることなく、計算リソースを活かしてより信頼性の高い最適解を導き出すことが可能になります。(※MultiRunの詳細は別記事でも解説しています。)
そのうち、ドーム状の形状に対する圧力解析でも実施してみる予定です。
- 相談が頻繁にある座屈を考慮した最適化設計の例
- 円錐殻の座屈
- 不定形状の圧力容器の座屈
- 高速走行時の風圧による、外装パネルの座屈
- 椅子等の垂直荷重+横荷重がかかる構造物 など
その解析課題、GRMが解決します。
本記事でご紹介した「座屈現象を考慮した最適化技術」や「動的な課題のCAE最適化設計」を、御社の製品開発に適用しませんか?
「現状のモデルを見てほしい」「テスト解析を依頼したい」など、技術的なご相談からでも大歓迎です。
※「記事を見た」と書いていただけるとスムーズです。
※技術のご相談は各事例モデルの解析担当者に対応させます。
この記事の監修・執筆チーム
GRM Consulting株式会社 解析エンジニアリング部
モータースポーツ最高峰のF1から量産車開発まで、20年以上にわたり構造設計・衝突・振動・流体解析に携わるスペシャリスト集団。 単なるシミュレーション結果の提示に留まらず、本記事のような座屈や圧壊の最適化設計を得意とし、性能目標の達成から軽量化まで様々な改善を手掛けています。
- 主要ツール:LS-DYNA, Abaqus, Genesis, Nastran, OptiAssist, Simcenter 3D
- 専門領域:構造最適化、衝撃エネルギー吸収体最適化、CFRP複合材解析、衝突解析、CFD解析
