【本事例紹介のトピック】
- 可動により荷重入力条件や伝達経路が変化するロボットアームに対し、複数の姿勢(ポジション)を同時に考慮したトポロジー最適化を実施
- クローニング制約(Cloning Constraint)を用いることで、異なる荷重ケースにおいても同一形状を維持する「製造可能な最適解」を導出
- サスペンションアームやリンク機構など、可動域を持つ構造部品の軽量化と剛性確保を両立する設計アプローチの検証
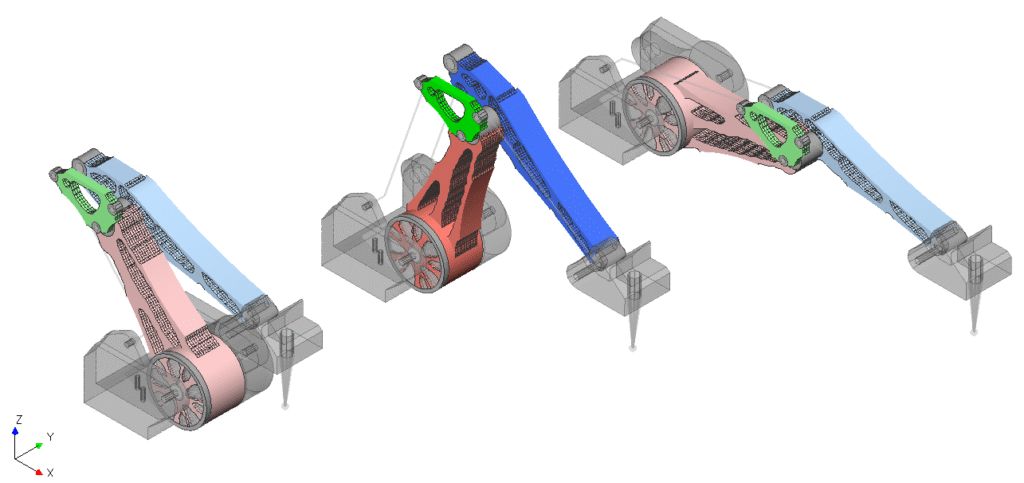
【クローニング制約検証用のロボットアーム解析モデル】
今回の事例紹介では、過去に紹介したクローニング制約条件を使用してロボットアームをトポロジー最適化してみます。基本的には全て過去の紹介事例と同様の流れとなり、より製品形状に近いものになっています。
アーム自体はSolid要素で作成し、リンクはBAR要素で簡略化します。すべての関節はMPCにより軸回転フリーの状態で接合しました。
下図の色付き部品が最適化対象部品です。
荷重条件は、アーム先端に複数方向からの荷重を与えます。
発生する応力分布が異なるため、そのまま最適化を実行すると3姿勢それぞれで別形状の結果になってしまうことが予想されます。

ポジション違いにより同じ入力荷重だったとしても受ける荷重の方向が変わってしまう。最適化を使用しない場合は、最も不利になる姿勢で強度/剛性検討することが一般的である。
【クローニング制約を使用しないトポロジー最適化】
まずはクローニング制約を使用しないでトポロジー最適化を実施してみます。当たり前ですが、3つの姿勢それぞれに対して剛性最大化をしようとするため、同一部品なのに別の形状になってしまいます。「これを元にして設計してね」と言われても困っちゃいますよね。

クローニング制約を使用していないため、3つの姿勢それぞれで別の形状となってしまい、同一形状同一製品にできない。
【クローニング制約を使用したトポロジー最適化】
クローニング制約を使用したモデルでは、腕が中間位置のものを「親」として最適化設定し、腕を畳んでいるものと伸ばしているものは「子」として取り扱います。(どれを親にしてもOKです)
親:中間位置のロボットアーム
子:畳んだ位置 と 伸ばした位置 のロボットアーム
クローニング制約を使用した場合の最適化結果を見てみましょう。

3つのポジション違いですべてのリンクが同一形状になっている。いずれの位置でも剛性の制約を満たす、最軽量の形状が導出される。
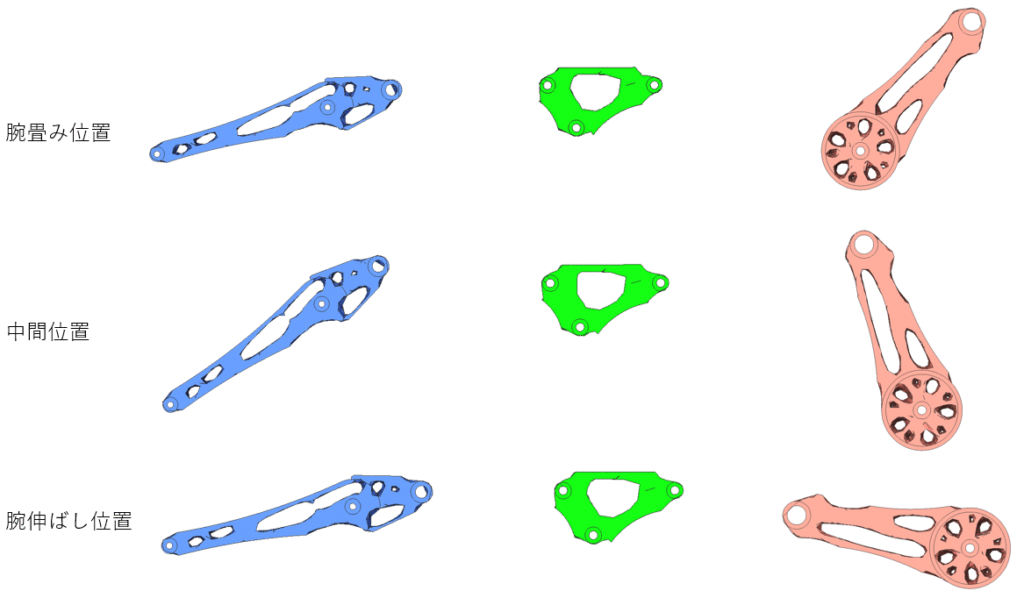
各リンクの形状詳細。いずれも同一形状であり、姿勢に関わらず一貫した形状である。複数姿勢を考慮した最も軽量な形状が導出できた。
ロボットアームがいずれの姿勢でも同じ形状として結果が出力されました。3姿勢すべての条件に対して、最も剛性が高くなる形状になっています。(「特定の姿勢での〇〇方向剛性」なども制約可能です)
【クローニング制約を使用することのメリット】
このように、クローニング制約を使用することで可動部品の最適化をすることができます。
トポロジー最適化に限らず、CAEによる最適化では様々な制約条件を使用することができます。製品の使用実態に合わせた制約条件の設定が重要です。
クローニング制約(Cloning Constraint)が有効な構造部品例
クローニング制約は、複数の異なる荷重条件や境界条件に対して、同一のトポロジー(位相形状)を導出する必要がある場合に推奨されます。特に以下のような製品・部品設計において強力なソリューションとなります。
- ロボットアーム / マニピュレーター: アームの姿勢(ポジション)変化に伴い、自重や把持荷重のベクトルが相対的に変化する構造体。
- クレーン等のブーム・ジブ構造: 伸縮や起伏角度によって支点距離やモーメントが変動する建設機械の主要構造部材。
- 自動車用サスペンションアーム: サスペンションジオメトリの変化(バンプ・リバウンド・操舵)により、入力荷重の方向が常に変化するリンク部品。
- 共通化部品(ブラケット類): 異なる車種や異なる取り付け位置で共有されるが、入力条件がそれぞれ異なるブラケットやステー。
- 連続パターン構造(柱・梁): 建築構造物やフレームなど、周期的かつ同一パターン形状で剛性を確保したい連続構造体。
- ホイール: 同一意匠のサイズ違い製品。オフセット量や直径の違いにより入力荷重や剛性目標値が変化する製品。
| 比較シチュエーション | 従来手法(制約なし)の課題 | クローニング制約のメリット |
|---|---|---|
|
姿勢違い(マルチポジション) ロボットアーム、サスペンション等 |
姿勢ごとに異なる最適形状が生成されてしまい、最終的にどの形状を採用すべきか(最大公約数的な形状はどれか)の判断が困難となる。 | 全ての姿勢(ロードケース)において共通化された「一貫した形状」が導出されるため、動作全域を満足する設計解が一度で得られる。 |
|
位置違い共通部品 共通ブラケット、左右対称部品等 |
「最悪条件」となる取付位置を事前に特定・定義する必要があり、想定外の入力による強度不足や、安全率の過剰な積み増しによる重量増を招きやすい。 | 全ての取付位置条件を同時に考慮して最適化するため、条件漏れや設計者の見込み違い(ヒューマンエラー)を防ぎ、確実に機能する共通形状を作成できる。 |
|
サイズ違いのシリーズ化 ホイール等の相似形サイズバリエーション等 |
サイズごとに異なる入力荷重や要件に対して個別に検証・修正を行う必要があり、シリーズ全体での設計工数が肥大化する。またデザインの統一性が保てない。 | サイズが異なっても「トポロジー(位相)」を統一する制約をかけることで、シリーズとしてのデザインアイデンティティを保ちつつ、工学的根拠のある形状を一括で設計可能。 |
この事例紹介では、ロボットアームの設計を題材にして、クローニング制約のメリットを紹介しました。実際の製品設計では製品や部品ごとに様々な個別の課題に直面していると思います。GRMでは20年以上にわたりCAE最適化設計のスペシャリストとして製品開発をしてきているので、お困りの際はお気軽にお問い合わせください。
その解析課題、GRMが解決します。
本記事でご紹介した「トポロジー最適化技術の応用」や「設計時間短縮ツール」を、御社の製品開発に適用しませんか?
「現状のモデルを見てほしい」「テスト解析を依頼したい」など、技術的なご相談からでも大歓迎です。
※「記事を見た」と書いていただけるとスムーズです。
※技術のご相談は各事例モデルの解析担当者に対応させます。
この記事の監修・執筆チーム
GRM Consulting株式会社 解析エンジニアリング部
モータースポーツ最高峰のF1から量産車開発まで、20年以上にわたり構造設計・衝突・振動・流体解析に携わるスペシャリスト集団。 単なるシミュレーション結果の提示に留まらず、本記事のようなCAE最適化設計を活かした設計を得意とし、製造要件(鋳造・鍛造・押出成形・板金・CFRP)を考慮した「造れる設計」を提案しています。
- 主要ツール:LS-DYNA, Abaqus, Genesis, Nastran, OptiAssist, Simcenter 3D
- 専門領域:構造最適化、衝撃エネルギー吸収体最適化、CFRP複合材解析、衝突解析、CFD解析
