非線形接触を使用したトポロジー最適化②

LS-TaSCによる梁の３点曲げトポロジー最適化結果

今回の事例では、以前公開した非線形接触を使用したトポロジー最適化と同じことを、LS-TaSCを使用して実施してみました。普段の業務ではLS-TaSCは使っておらず、バージョンアップした際などにベンチマークしている程度なので、あまり良い設定で計算できていないかもしれません。

境界条件と入力条件は前回のGenesisによる最適化と同様とし、LS-Dynaの解析モデルを作成しました。材料の降伏点を超えるほどの荷重は与えていないため、前回の非線形接触を使用した解析結果と同じ変形量、変形モードになります。

LS-TaSCでトポロジー最適化するためのLS-Dyna梁の３点曲げ計算モデル

今回は以下３つのアルゴリズムで計算したものを比較します。

  1. True Mechanics：エネルギー密度を考慮する（≒衝突や非線形モデル向け）
  2. SIMP（LS-TaSC）：材料密度（剛性）を考慮する（≒線形静的モデル向け）
  3. SIMP（Genesis）：前回の事例モデル

単純な梁の３点曲げをSIMP法とTrue Mechanics法でトポロジー最適化した結果形状の比較

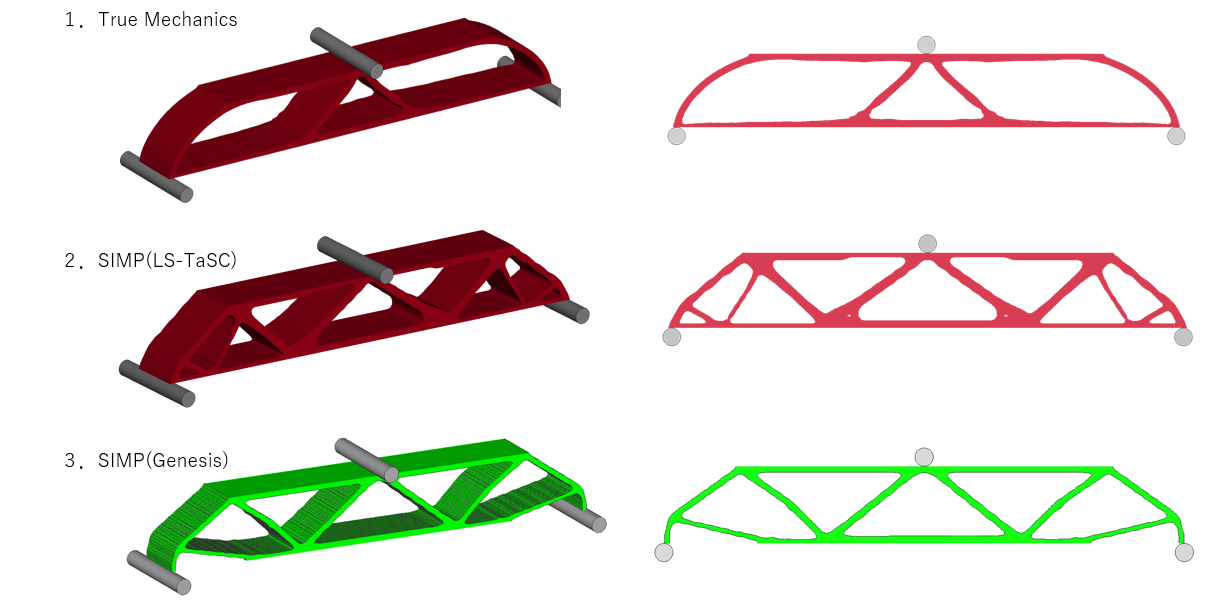
いずれのモデルもMF（マスフラクション）を0.2としていますが、LS-TaSCによる最適化結果はどうにもMF0.2に見えません。なお、Genesisの結果はほぼ正確に元の体積の20%になっています。

  1. True Mechanics
    設定したMFよりも小さくなっています。圧子を受ける部分は他と同じ形状です。ImplicitソルバーよりもExplicitソルバーで真価を発揮しそうです。
  2. SIMP (LS-TaSC）
    設定したMFよりも大きくなっています。（MF0.3くらいの体積）Genesisの結果と非常によく似た結果になります。MFの設定どおりの計算結果であれば、Genesisと同じ結果になりそうです。

以前から、LS-TaSCでは制約条件に対し過剰な結果が返ってくる傾向にあるようです。（ボンネット構造の最適化参照）

しかし、非線形接触が取り扱える最適化ソルバーは少ないため、LS-Dynaユーザーには使い勝手の良い最適化ソルバーと言えるかもしれません。

なお、計算時間はGenesisによる線形静的な最適化の5~10倍くらいかかります。

 

LS-TaSCで動的課題をトポロジー最適化してみる

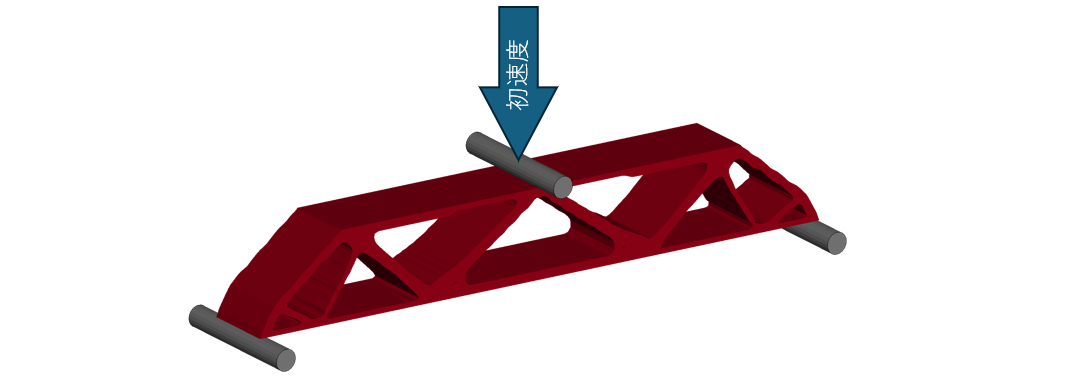
次回の事例紹介では、ちょっとイマイチな結果になったTrue Mechanics法を、上図のようなExplicit解析で実行してみます。